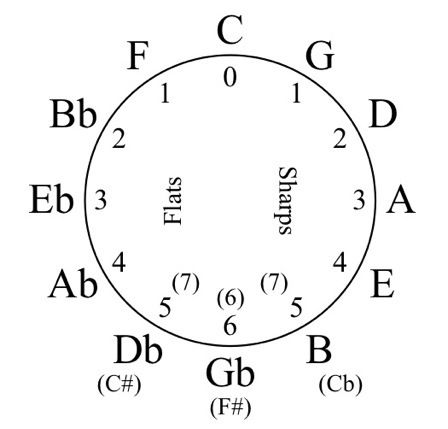
Suppose we take the 15 written major keys and put them in a straight line, beginning with 7 flats on the far left, moving toward C (no sharps or flats), and then continuing to 7 sharps on the far right.
7b, 6b, 5b, 4b, 3b, 2b, 1b, 0, 1#, 2#, 3#, 4#, 5#, 6#, 7#
The names of the keys would be...
Cb, Gb, Db, Ab, Eb, Bb, F, C, G, D, A, E, B, F#, C#
Then imagine we wrapped this straight line around a clock with C at the top. (Because there are 15 keys represented on the line, and only 12 places on the clock, there will be a little bit of an overlap at the bottom.)
The resulting figure is called the "Circle of Fifths." In music theory, we call the interval from C to G a fifth, because G is the fifth note in the C major scale. D is the fifth note in the G major scale, and so on around the circle.

Learning the Circle
There will come a time, if you keep learning, playing, and writing, when you will know the circle of fifths because you will have spent time in all the keys, but when seeing it for the first time, it may help to have a few tricks. This is how I teach it to beginning students.
C and F
First, there are two locations you will just have to memorize: C, which is easy because it's zero, and F. To remember F, say this. "Flat has one F, and F has one flat."
G, D, A, E, B
The second group is G, D, A, E, and B. These are keys with sharps. To remember how many sharps each one has, just look at the letter. It takes a little imagination with G, but if you are willing to round the corners a bit, you can sort of draw a G with just one stroke of the pen.

Writing a D takes 2 strokes of the pen... an A takes 3 strokes... an E takes 4 strokes... and B... you can write the number 5 on top of a B without ever wandering off of the letter.
This is one way to remember that G is 1 sharp... D is 2 sharps... A is 3 sharps... E is 4 sharps... and B is 5 sharps.

Bb, Eb, Ab, Db, Gb
Once you get used to the sharp keys, the flats use the "add up to seven" rule. Like this: if G is 1 in your mind, then when you drop the symbol for flat into the picture (Gb), add enough to get a total of 7. In this case, you would need to add 6. So Gb is 6 flats. Or more simply, "G is 1 sharp, so Gb is 6 flats."
Let's try that with another letter: Db. You know D is 2 sharps, because it takes two strokes of the pen. Putting the flat in means we have to add up to seven, so we're looking for a 5. Therefore Db is 5 flats. Reducing it down, we get, "D is 2 sharps, so Db is 5 flats."
The same thing works for A, E, and B.
We can say the following:
G takes 1 stroke of the pen, so G is 1 sharp.
Therefore Gb is 6 flats. It adds up to seven.
D takes 2 strokes of the pen, so D is 2 sharps.
Therefore Db is 5 flats. It adds up to seven.
A takes 3 strokes of the pen, so A is 3 sharps.
Therefore Ab is 4 flats. It adds up to seven.
E takes 4 strokes of the pen, so E is 4 sharps.
Therefore Eb is 3 flats. It adds up to seven.
B can have a 5 written on top of it without ever leaving the B, so B is 5 sharps. Therefore Bb is 2 flats. It adds up to seven.
Cb, F#, C#
Finally, the three extra keys. The rule of seven still works.
Because F is 1 flat, F# is 6 sharps.
Because C is zero, C# is 7 sharps, and Cb is 7 flats.
Something Else About the Circle
Another interesting thing about the circle is that it's possible to write songs that use part or all of the circle as a progression. For example, you could start with a C chord, move to F, follow that with Bb, and keep going until you get back to C. Or you could write a song using the progressions we explored in the maps, and somewhere in the middle of the song use a part of the circle. For example, you could use B - E - A - D - G - C.
(Side note: when I was studying music, one of my teachers assigned keyboard drills that went around the circle. For example, we would take a major 7 chord in root position (notes 1-3-5-7), and play it in both hands at the same time. So for CM7 we would play c-e-g-b in the left hand and c-e-g-b in the right hand; eight notes at once. Then we would play it around the circle - CM7 (cegb) - GM7 (gbdf#) - DM7 (df#ac#) - AM7 (ac#eg#) - until we got back to CM7. If you would like the same challenge, choose a chord, play it in both hands, and then take it around the circle.)
The “Photographic Opposites”
There are four sets of scales (D and Db, E and Eb, A and Ab, B and Bb) which might be easier to memorize if you realize they are like photographic negatives of each other.
Look at D and Db for a moment. Notice the D scale has black notes at positions 3 and 7. In the Db scale, there are white notes at positions 3 and 7.


The same idea can be seen with E and Eb, A and Ab, B and Bb. Notice how they mirror each other, but the colors are opposite.






What this means is when you learn to play one of them, you may want to spend a little time and learn the corresponding one also.
Let’s Review
In parts 6, 7, 8, and 9, we spent some time looking at major keys and the major scale. We thought about the names of the notes, and the fact that numbers can be associated with each scale position.
We illustrated these scales, and we demonstrated that the names of the major keys can be wrapped around a circle called the Circle of Fifths.
Our goal is to learn to play these scales, explore melodies using these scales, and eventually write songs in these keys. If you continue learning, someday each of these scales and keys will be a comfortable place to play. Along the way, remember to enjoy the process. Take your time, learn well, and have fun!
When these discussions on major scales are understood, continue on to Part Ten.
OTHER RESOURCES
PDF eBook
The materials presented in Section 1 (Parts 1-12) are available as a downloadable PDF eBook. Click for more information.
Yours To Play It
...free, interactive, chord-exploring MIDI controller app for
Windows computers.
ChordMapMidi
...interactive, chord-exploring MIDI controller app for iPhone.
ChordMaps2
...interactive, chord-exploring MIDI controller app for iPad.
CarolPlayMidi (Christmas Carols and Hymns), DrumMapMidi (basic
drum patterns), and PowerPlay5 (play power chords on iPhone) are
our other iPad and iPhone MIDI controller apps.
______________________
Music Theory for Songwriters is part of MugglinWorks.com
Build a free web page with Mobirise