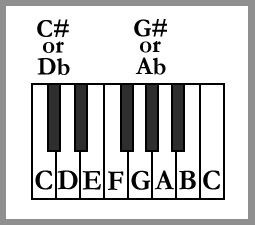
Concept - Sharps and Flats
On a keyboard, moving one half step to the right (going higher in pitch) is called "sharp," and moving one half step to the left (going lower in pitch) is called "flat."
The symbol for sharp is # and the symbol for flat looks a little like a lower case “b.” (It’s not exactly a “b,” but it’s similar, so we’ll use the symbol “b” in our discussion.)
Each black note has two names.
The note between C and D is either C sharp or D flat.
The note between D and E is either D sharp or E flat.
The note between F and G is either F sharp or G flat.
The note between G and A is either G sharp or A flat.
The note between A and B is either A sharp or B flat.

(To be complete, there are also times when certain white notes can be named sharp or flat. It doesn't happen very often, but there are occasions when the note B might be called Cb, or the note C might be called B#. E and F work the same way. It’s also possible to have double sharps (written x) or double flats (written bb). For example, Fx would mean play the note G, and Gbb would mean play the note F.)
Now that we understand sharps and flats, let's look at another scale.
The G Major Scale
If you begin by playing the note G and then follow the formula for the major scale (WWHWWWH), you will get the following...
G, A, B, C, D, E, F#, G.

Take a look at the G scale. Which note is number 5? Which letter is associated with number 3? Could you play the sequence 6, 5, 8, 3, 2, 5, 1?
(Side note: one of the rules of naming notes in a major scale is that each letter from A to G must be assigned as you move from note 1 up to note 7. That's why note 7 in this scale is called F# and not Gb.)
Above and Below the Scale
Although some songs can be played using only notes 1 through 8, many songs go above or below the scale at some point. This would be a good time to say again that note 8 is really note 1 starting over. We say it's note 1 moved up an “octave.” So, even though we say 1, 2, 3, 4, 5, 6, 7, 8, we understand that it really goes 1, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7 and so on.
This creates a question when writing down melodies as numbers. If you are asked to play 1, 2, 7, do you play the 7 that's a big jump up the keyboard, or do you play the 7 that's right next to 1 on the left side?
In order to make this clearer, I’ll write the notes in the next octave down as underlined numbers, and the notes in the next octave up as numbers with lines through the middle. Now our system looks like this.
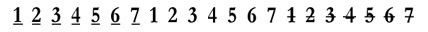
Why Do We Use Numbers?
The nice thing about numbers is that when we change to a different major scale, though the letter names at the various locations change, the numbers stay the same. So, if a melody is played 3, 5, 2, 3, 1 in one major key, it will be played 3, 5, 2, 3, 1 in the other major keys as well.
It's true that the phrase played will sound higher or lower in pitch when you move it to a new key, and the letter names associated with note 3, or note 5, or note 2 will be different in the new key, but the tune will sound the same.
One suggestion is to experiment with the notes in a scale until something you play reminds you of a song you already know. Then see if you can figure out a couple phrases from that particular song. Play it a few times in the key you are in, and write down the numbers using the system just explained. Then take those numbers and play them in another key of your choice. This exercise will show you how melodies keep the same numbers when they are played in different keys.
One Important Idea to Consider
There is another idea to consider, because in the long run it will be more and more valuable to you. As you play tunes you know, and as you experiment writing your own melodies, you will eventually begin to "recognize the numbers" even when they are not written down. You will hear the notes in your mind, and recognize almost by "feel" which number comes next. You'll hear a song, and know which notes to play. You will begin to improvise music freely, and make tunes up spontaneously. Then music becomes a lot of fun!
Let’s Review
In this section we discussed sharps and flats. The symbol for sharp is #. It indicates a note one half step higher in pitch (to the right on a keyboard). The symbol for flat is similar to b. It indicates a note one half step lower in pitch (to the left on the keyboard). These definitions allow us to name the black notes, each of which has two names. Named as sharps, the black notes are C#, D#, F#, G#, and A#. Named as flats, the black notes are Db, Eb, Gb, Ab, and Bb.
When naming the notes in a major scale, we use each of the letters from A to G on scale notes 1 through 7. This determines whether black notes are named as sharps or flats.
We looked at the G major scale. We now have two scale pictures, one for the C scale, which is all white notes, and one for the G scale, which has a black note at position 7.


We also thought about the idea that a melody may go above or below scale notes 1 through 8. To write these other notes down, we introduced underlined numbers for the octave to the left, and numbers with a line through the middle to indicate notes in the octave to the right.
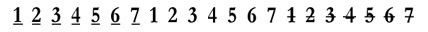
We considered the possibility of exploring a phrase in a given key, writing down what we played as a sequence of numbers, and then playing the same phrase in another key.
We also considered the idea that someday we may be able to hear a tune and know which notes to play, because the sound of the various numbers, and the jumps between them, will have become recognizable.
You may want to experiment with these ideas. Then move on to Part Eight.
OTHER RESOURCES
PDF eBook
The materials presented in Section 1 (Parts 1-12) are available as a downloadable PDF eBook. Click for more information.
Yours To Play It
...free, interactive, chord-exploring MIDI controller app for
Windows computers.
ChordMapMidi
...interactive, chord-exploring MIDI controller app for iPhone.
ChordMaps2
...interactive, chord-exploring MIDI controller app for iPad.
CarolPlayMidi (Christmas Carols and Hymns), DrumMapMidi (basic
drum patterns), and PowerPlay5 (play power chords on iPhone) are
our other iPad and iPhone MIDI controller apps.
______________________
Music Theory for Songwriters is part of MugglinWorks.com
Mobirise free software - More