
Imagine for a moment that time rolled backwards and you found yourself in a chapter in history where they hadn’t yet discovered the sharps and flats, and "pianos" (which wouldn't have been around yet, but if they had been) had only white notes, and the only major scale available was C.
So you accepted those limitations, and wrote a few songs in the key of C major, but then you wanted a new sound, something that would be different. So you looked down at your hands, and the thought came, "What if I shifted my hands one note to the right?"
Let me pause here to correct a possible misunderstanding. In our modern world of music, we have a concept called "transposing." By it we mean that we can take a song and move every note up (or down) by a certain number of half steps. When we do this, the result is a little higher (or lower), but because we shifted every note the same amount, the song still sounds like it did before. The relative jumps from note to note have not changed.
Now, back to the "unusual piano missing the black notes.” We know that the jumps from note to note in the C major scale follow the formula whole - whole - half - whole - whole - whole - half. In other words, the distance from note 1 to note 2 is a wider gap than from 3 to 4. So even though our unusual piano may look to our eyes as though each note is evenly spaced, we know in the world of sound and frequencies it isn't that way.
Perhaps we can say it like this: just because the black notes have not yet been discovered doesn't mean they are not there. We still have to leave a space for them in our minds, because we know they will come along later.
So you shifted your hands one note to the right and played one of the songs you had written in C major, but now, because the whole and half step jumps are at a different place under your hands, this new version of your song sounded quite different.
Great! We wanted a different sound. That was the purpose of shifting the song in the first place.
So you stepped back for a minute and asked, "What was it I just did?" And then you realized that you took the original key of C major (where we number the notes 1, 2, 3, 4, 5, 6, 7 - with the note C being note 1, D being note 2, and so on), and "renumbered" it so the D is now note 1, E is note 2, etc.
Then you realized there was nothing to stop you from shifting again. What if E was note 1, or F, or G? In fact, there are seven different notes, any one of which could be note 1. Therefore you could play your song in seven different places, the original (in C major) and six other places, by shifting the song to the right.
When this grows clear in your thinking, there's something else important to grasp. We used the key of C major in our example, because it's easy to see that all the notes are evenly spaced, and you can imagine shifting your hands one note to the right without any difficulty. But coming back into the present, we could have used any of the 12 major keys on our modern piano.
For example, the key of Db major has 5 black notes and 2 white notes. Keep those 7 notes, and remove the rest. Now 5 white notes are missing. It's not as easy this time to play the same song while shifting, because the scale notes, being both black and white, are not spaced evenly. Still, with practice, you could probably do it. And you could renumber the notes just like we did before; the math isn't any harder.
What this means is any song (using only scale notes) written in any of the 12 major keys can be played in its original location (where note 1 is the name of the key), and can also be played six other ways, each time shifting the hands one more scale note to the right, and renumbering the keys so that note 1 is at a new place.
This idea of shifting the notes needed some names, and so the ancient Greeks (because they were thinking about this) gave each of these locations a name.
IONIAN
Played in the original major scale.
DORIAN
Played one scale note to the right.
(The original note 2 is now note 1.)
PHRYGIAN
Played two scale notes to the right.
(The original note 3 is now note 1.)
LYDIAN
Played three scale notes to the right.
(The original note 4 is now note 1.)
MIXOLYDIAN
Played four scale notes to the right.
(The original note 5 is now note 1.)
AEOLIAN
Played five scale notes to the right.
(The original note 6 is now note 1.)
LOCRIAN
Played six scale notes to the right.
(The original note 7 is now note 1.)
Thinking This Through
To think this through and understand what's happening, first you need to know the major scale pictures we looked at back in parts 6, 7, and 8. Second, you also have to know that Ionian mode is associated with note 1 of the major scale, Dorian with 2, Phrygian with 3, Lydian with 4, Mixolydian with 5, Aeolian with 6, and Locrian with 7.
Knowing these two things, you can then work through an example.
A DORIAN - We'll take A Dorian as our example. We know that Dorian is built on note 2 of the major scale. Which major scale has A as note 2? The answer is G. The G major scale is the place where we will find A Dorian as one of the possible "shifts." So far, so good.
Now, what about the scale? We remember the G major scale starts on note G and climbs through the notes A, B, C, D, E, and F#. Also, these notes are numbered in our minds. G is 1, A is 2, and so on up to F#, which is 7.
To play A Dorian we play the same notes, but now A is 1, B is 2, all the way up to G, which is now 7. So the scale is A, B, C, D, E, F#, G, A.
Next, which chords are available. Again we use what we already know about G major. The basic chords found in G major are G, Am, Bm, C, D, and Em. (There is one more, the vii chord, which is F# diminished. You may include this chord if you like, but you'll probably find yourself using the first six chords a lot and the vii chord less often.) Because we are in Dorian, the Am chord is now the "home" chord, and the other chords are available to use in progressions.
Some progressions would come to you right away: Am-G-Am, or Am-Em-Am, or Am-C-D-Am. With a little experimenting, you might discover quite a few more. These are your building blocks then for writing songs in A Dorian.
You might wonder, "Do I need a big map for A Dorian?" The answer is no. Remember, there are five notes missing from each octave of the piano, so chords which might have used those extra five notes are not available. This knocks out a lot of possibilities. Playing just the six chords (or seven if you use the vii chord) keeps you in the mode.
Another Way of Thinking About It
There is another important way to consider this idea.
Suppose you are playing an instrument, perhaps an instrument that plays just one note at a time, and you don't want to associate A Dorian with the G major scale, because that takes a little time to think about. In fact, as soon as you hear the name A, you picture the A scale. So you would rather hear the word Dorian as indicating a change to be made to the A major scale, which was already in your mind as soon as you heard the name A. Somehow we've got to get to the A Dorian scale, beginning with the picture for the A major scale.
To do this we compare the A Dorian scale (A, B, C, D, E, F#, G) to the A major scale (A, B, C#, D, E, F#, G#). Notice the differences are in notes 3 and 7. Both are down a half step in the Dorian version. So we could make a "rule" to memorize. We'll use X as a variable, as in math, to stand for any note on our modern keyboard. Here's the rule - "To play X Dorian, play the X major scale with notes 3 and 7 down a half step."
The “Rules”
This idea of memorizing rules can be applied to the other modes as well. These rules, and a fairly intuitive way of deriving them, are listed here.
IONIAN
Played in the original major scale.
DORIAN
Played one scale note to the right.
(The original note 2 is now note 1.)
Another way of thinking about it...
X Dorian - play the X major scale with notes 3 and 7
down a half step

To remember this rule, picture the D major scale.
Notice that notes 3 and 7 need to be lowered to lose all the sharps and flats.
PHRYGIAN
Played two scale notes to the right.
(The original note 3 is now note 1.)
Another way of thinking about it...
X Phrygian - play the X major scale with notes 2, 3, 6, and 7
down a half step

To remember this rule, picture the E major scale.
Notice that notes 2, 3, 6, and 7 need to be lowered to lose
all the sharps and flats.
LYDIAN
Played three scale notes to the right.
(The original note 4 is now note 1.)
Another way of thinking about it...
X Lydian - play the X major scale with note 4
raised a half step

To remember this rule, picture the F major scale.
Notice that note 4 needs to be raised to lose all
the sharps and flats.
MIXOLYDIAN
Played four scale notes to the right.
(The original note 5 is now note 1.)
Another way of thinking about it...
X Mixolydian - play the X major scale with note 7
down a half step

To remember this rule, picture the G major scale.
Notice that note 7 needs to be lowered to lose all
the sharps and flats.
AEOLIAN
Played five scale notes to the right.
(The original note 6 is now note 1.)
Another way of thinking about it...
X Aeolian - play the X major scale with notes 3, 6, and 7
down a half step

To remember this rule, picture the A major scale.
Notice that notes 3, 6, and 7 need to be lowered to lose
all the sharps and flats.
LOCRIAN
Played six scale notes to the right.
(The original note 7 is now note 1.)
Another way of thinking about it...
X Locrian - play the X major scale with notes 2, 3, 5, 6, and 7
down a half step

To remember this rule, picture the B major scale.
Notice that notes 2, 3, 5, 6, and 7 need to be lowered to lose
all the sharps and flats.
Experimenting with Modes
If you would like to experiment with modes, one of the easiest ways is to look at the chart we saw earlier in these lessons. Here it is again.
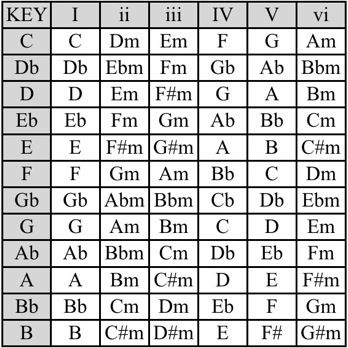
Take the six chords from any line (adding chord vii if you wish - it will be a diminished chord whose root is the seventh note of the major scale). Then choose a chord other than I as "home."
Explore the various progressions you can create using these six (or seven) chords. Keep in mind which chord is the home chord and keep coming back to it to establish that sound.
When chord I is home - Ionian.
When chord ii is home - Dorian.
When chord iii is home - Phrygian.
When chord IV is home - Lydian.
When chord V is home - Mixolydian.
When chord vi is home - Aeolian.
When chord vii is home - Locrian.
Each mode has its own feel. If you do this simple experiment, spending some time in each mode, your musical horizons will expand.
Let’s Review
In this section we explored the concept of modes. We discussed where they come from, what we call them, and how to think about them.
From a chord perspective, we looked at the six (or seven) chords needed to write songs in the various modes. We are using the same chords we were using in major (Ionian), but the sound and feeling are new because a different chord is considered to be home. Also, because the notes in the scale are sometimes a whole step apart and sometimes a half step, shifting the scale puts the half steps in a different place. This helps produce the new sound and feel.
From a melodic perspective (for single note instruments, or for single note lines played on chordal instruments), we recognize that a player can memorize the major scales and think of the modes as changes to be made to the scales. In certain musical situations, this will be faster than trying to think of which major scale the mode comes from. To address this, we introduced "rules", and suggested a way to derive the rules in your mind using the major scale pictures for D, E, F, G, A and B. Each of these pictures shows which notes must be changed to create a certain modal scale.
We then considered the idea of spending some time in each mode, exploring how the various home chords affect the feel of the progressions. Creating several progressions in each mode will help expand your songwriting resources.
On to Part Eleven.
OTHER RESOURCES
PDF eBook
The materials presented in Section 1 (Parts 1-12) are available as a downloadable PDF eBook. Click for more information.
Yours To Play It
...free, interactive, chord-exploring MIDI controller app for
Windows computers.
ChordMapMidi
...interactive, chord-exploring MIDI controller app for iPhone.
ChordMaps2
...interactive, chord-exploring MIDI controller app for iPad.
CarolPlayMidi (Christmas Carols and Hymns), DrumMapMidi (basic
drum patterns), and PowerPlay5 (play power chords on iPhone) are
our other iPad and iPhone MIDI controller apps.
______________________
Music Theory for Songwriters is part of MugglinWorks.com
Created with Mobirise page maker